众所周知，浮点数与整形类型在相互转换后可能发生的精度丢失问题。浮点数转换为整形会发生截断和溢出问题，整形转换为浮点型会发生精度丢失问题。究其原因，是浮点型和整形在存储模式上的差异导致的。

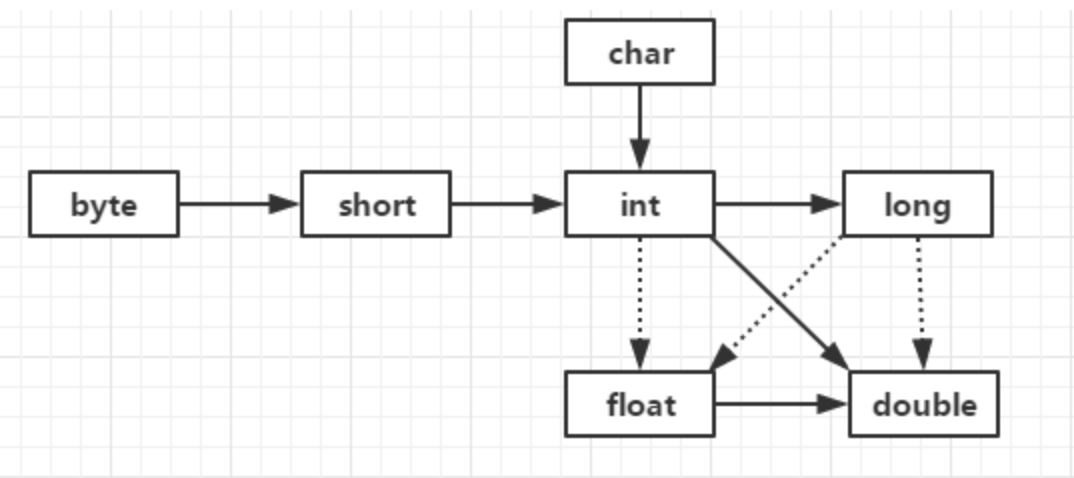Java类型转换时可能发生的精度丢失（虚线代表该转换存在精度丢失问题）

整形与浮点数的存储模式

计算机内部的所有数据都是用二进制编码来存储的。比如，7 可以用 0111 来表示。对于整形类型，整数类型可以根据占用的空间大小分为 int8，int16，int32 和 int64，不同的编程语言对它们有不同的命名方式。它们的区别在于占用的位数不同，例如，int32 占用了 32 位（也就是 8 个字节），这也决定了它们能表示的整数范围不同。

例如对于数字 7，int32 的底层是这样表示的：0000 0000 0000 0000 0000 0000 0000 0111

但与整型不同，浮点数的存储方式是把数据分成两部分，一部分是尾数，一部分是指数。比如，小数 25.125 可以用二进制表示为 11001.001，就是把整数部分和小数部分都转换成二进制。

但是这样存储在计算机里面不方便，除非用一些位来记录小数点的位置（指数），否则我们无法确定 1000 1001 这个二进制数代表什么。它可能是 1.000 1001（1.0703125）、10.001001（2.140625）或者其他的值。

浮点数的特点是小数点的位置不固定，而是由指数来决定，这就是浮点数的含义。任何一个小数 \(V\) 都可以写成 \(1.???? \times 2^?\) 这样的形式，或者更准确地说：

\[V = (-1)^S \times M \times 2^E\]

其中，\(S\) 是符号位，表示正负号；\(M\) 是以整数部分为 1 的小数；\(E\) 是指数，表示小数点的移动位数。为了节省空间，浮点数存储时只会存储 \(M\) 的尾数，即小数部分。

例如， 25.125（11001.001）就可以表示为 \(1.1001001 \times 2^4\) ，对应的有 \(M=1.1001001\)，\(E=100\)（二进制）。

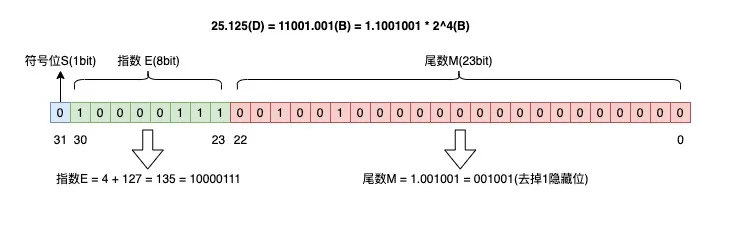32位浮点数表示25.125（尾数指小数部分）

float32 类型是一种浮点数，它用 32 位（也就是 4 个字节）来存储一个小数。它的存储方式是把这 32 位分成三部分，第一位是符号位，表示正负号；后面 8 位是指数位，表示小数点的位置；最后 23 位是尾数位，表示小数的精度。

我们可以算一下，float32 能表示的最小精度是 \(2^{23}\)，能表示的最大值是 \(2^{128}\)，也就是 3.4e+38。但是这样有一个代价，就是浮点数不能精确地表示所有的小数。因为有些小数转换成二进制后是无限循环的，比如 0.1，它的二进制表示是 0.0001 1001 1001 1... 。这样就会有一些误差，就像用栅栏来划分数轴一样，有些数会落在栅栏之间，就要取最近的一个栅栏来表示。所以用二进制浮点数来表示小数都会有一定的误差。

精度丢失的本质是，浮点数存储方式无法在有限的空间中精确的表示该值。

整型转浮点数

整型使用二进制直接表示一个数，当我们将整型转换为浮点型时，其底层的存储方式也会相应的发生变换。这一过程直接导致了精度的丢失。实际上，浮点型能过表示的数值范围远大于整型。

我们以 int（int32）转 float（float32）为例：

假设一个足够大的 int32 数 1234567890（二进制 100 1001 1001 0110 0000 0010 1101 0010），其浮点表示为 \(1.001001100101100000001011010010(30bits) \times 2^{11110(5bits)}\)。为精确表示这个数，需要 30bits 的空间存储尾数，5bits 的空间存储指数。然而，float32 的尾数部分仅有 23bits。

为将该数存储到 float32 中，我们只能舍弃掉后面 7bits 的信息。假设使用截断方式进行舍弃，那么 1234567890 在 float32 中的浮点数表示为 \(1.00100110010110000000101(23bits)\times 2^{11110(5bits)}\)，也就是是 100 1001 1001 0110 0000 0010 1000 0000，其十进制为 1234567808。与原始值的差为 82）。

由于精度上的考虑，实际上存储时可能不是简单的进行截断。实际上，数 1234567890 在 Java 的 float 类型中的存储值是 \(1.00100110010110000000110(23bits) \times 2^{11110(5bits)}\)，也就是 100 1001 1001 0110 0000 0011 0000 0000。其十进制为 1234567936。与原始值的差为 46）。

从数学上说，浮点型数据是用二进制的科学计数法来压缩表示数值的。我们把科学计数法中从左边第一个不为 0 的数字开始，一直到末尾数字结束（不包括幂次部分）的部分定义为有效数字。有效数字反映了数值的大小和精确度。浮点数的首位一定是 1，所以我们可以认为浮点数的尾部就是它的有效数字。浮点数的尾数长度决定了浮点数的存储精度。如果一个整型数值使用科学计数法表示后，它的有效数字比浮点数的尾部更大，那么该数由整型转换成浮点类型时就必然会出现精度损失。

也因此，精度丢失的本质是，浮点数存储方式无法在有限的空间中精确的表示该值。

参考内容：

浮点数类型转换时的精度丢失问题

整形与浮点数的存储模式

整型转浮点数

CATALOG